Reflect Family

1 Warm-Up

After you master the challenge on page 1, you can try slightly harder challenges on pages 2 and 3.

Loading...

✏️ What do you notice? What do you wonder?

✏️ Is this page easier or harder than page 1? What makes it different?

2 Reflect Dance 1

Physical Dance

Work with a partner to perform two short reflect dances, moving as if there is a mirror between you. To locate the mirror, put a piece of tape on the floor, with a dance guide paper in the middle of the mirror like this:

For the first dance, flip a coin to identify one person as the independent dancer and the other as the dependent dancer. You will switch roles for the second dance.

Independent Dancer: Always look at your partner, and take steps according to the directions below. As you dance, you can do any other body movement that’s both safe and simple enough that your partner can mirror it. Start one step back from the middle of the mirror.

Dependent Dancer: Mirror your partner’s movements, staying exactly across the mirror from your partner and the same distance away from the mirror.

First Dance:

3 steps south
6 steps west
4 steps northeast
3 steps southeast

Draw a diagram to show the path that each of you followed.

Describe the relative directions you moved in each part of the dance.

Second Dance:

3 steps southeast
2 steps north
3 steps southwest
Improvise and record the rest of your dance routine

When did you both move in the same direction? When did you move in opposite directions?

Virtual Dance

Loading...

Hint Video:

Hint Videos:

Drag the independent variable (the penguin) so that the two dancers make an interesting pattern.
Use the Trace Widget to erase the traces.
Make another interesting pattern.
What do you notice about the relative directions of the dancers?
What do you notice about the relative speeds of the dancers?
Can you find any fixed points? If so, where are they?

Drag the independent variable to follow the gray domain.
You can use the Trace Widget to erase the traces and start again.
What do you notice about the shape of the domain and the shape of the range?

Try at least four of the Step tools to see what they do.
When the penguin moves east (E), which way does the frog move?
When the penguin moves south (S), which way does the frog move?
Erase your traces.
Try the Plot tool. What does it do?
What does the Dance tool do?
Use the Undo and Redo arrows to undo the last tool or redo the next tool.

Press the Step tools to make the penguin follow the domain marked in gray.
Use the Undo and Redo arrows to fix any mistakes you make.
When you finish, use the Dance tool to make the variables dance using your domain.
When the penguin moves north-east (NE), which way does the frog move? Why does it move in this direction?

Use the Step tools to make the frog follow the given range.
Use the Dance tool to make the dependent variable dance along the range.
Why was it harder to make the frog follow a given range than to make the penguin follow a domain?
Why was it even harder to make the dependent variable follow this given range?

Use the Step tools to choreograph a domain and range of your choice.
Make part of your domain go above the mirror.
Use the Dance tool to make the variables dance using your choreography.
What would happen if two real human dancers tried to get to the other side of the mirror?

Use the Free Style tool to choreograph a domain and range of your choice.
Double-tap the Free Style tool to make it stay active. Tap it again to turn it off.
Use the Dance tool to make the variables dance using your choreography.
When you finish, draw and label a picture to show the mirror, your domain, and your range.

3 Construct Reflect Functions

Loading...

Hint Videos:

Hint Video:

Create an independent variable, a function rule, and a dependent variable.
Drag `x` around. What three objects did you use to create this function?
Drag `x` again. What do you notice about the relative speed and direction of `x` and `r_m(x)?`
Turn on tracing for `x` and `r_m(x)` and draw an interesting shape.
In your shape include parts where you drag `x` toward and away from mirror `m` and parts where you drag it parallel to mirror `m.`
You can use the Style Widget to change the color and size of the variables and the mirror.
Draw a picture of your traces. Show the mirror in your drawing.

You and your partner should each create a design and submit your own drawing to your teacher.

On page 1, you used three tools:

the Independent tool created independent variable `x,`
the Rule tool created the mirror, and
the Dependent tool created dependent variable `r(x).`

These three tools emphasize the three parts of a function: the independent variable, the function rule, and the dependent variable.

On this page you’ll use the Reflect tool to create all three parts of the function. When you use it, keep in mind the three different things it makes.

Use the Reflect tool to construct a reflect function.
Turn on tracing for both variables.
Adjust the function rule so that you can drag `x` to make the two variables trace out the background image.
Draw a picture of your traces. Include the labels of the variables and the mirror.

Use a reflect function to trace a different letter.

List other letters you could trace using a reflect function, showing the mirrors.
Pick a letter and use one of the Domain tools to make the shape of half of your letter.
Use the Vary x tool to restrict `x` to your domain and create a Vary x button.
Reflect `x` across a mirror.
Turn on tracing for both variables.
Press the Vary x button to make the variables dance.
Adjust the function rule and the domain to get the shape of the dance just the way you want it.
After adjusting, use the Visibility Widget to hide the domain and the mirror.
Erase your traces and then press the Vary x button to vary `x` along its hidden domain.
Draw a picture of the dance. In your picture, show the two variables, the domain, and the mirror.

The fixed points of a function are the places where the independent variable `x` and the dependent variable `r_j(x)` come together.

Use one of the domain tools and construct an interesting reflection with multiple fixed points. (Your result can be a letter of the alphabet, or some other shape of your choice.)
What do you notice about these fixed points? What do you wonder?
What do you think the symbols `r_j(x)` represent?
Experiment with the Label Widget to see how it works.
If you saw a dependent variable labeled `r_p(z),` what do you think this label would mean?

Construction Challenge 1

Create a domain and use the Vary x tool to restrict variable `x` to your domain.
Reflect independent variable `x` across two different mirrors, `j` and `k.`
Turn on tracing and vary `x` to make an interesting design.
Can you think of two different ways to construct the two reflections? Describe them.
Make a drawing of your result. Include the labels for the mirrors and variables.

Construction Challenge 2

On this page, figure out how to construct these dependent variables: `r_j(r_k(x))` and `r_k(r_j(x)).`
Describe in words what these two labels mean.
How can you arrange `j` and `k` so that `r_j(r_k(x))` and `r_k(r_j(x))` lie on top of each other?
Make a drawing of your result. Include labels.

Construction Challenge 3

On this page, put `x` on a restricted domain of your choice, and construct `r_k(r_j(x)).`
Arrange `j` and `k` so that `r_k(r_j(x))` stays on top of `x` when you vary `x` on its domain.
How did you do it? Draw your result.

4 Find the Rule

Loading...

Hint Video:

These traces were left behind by an independent variable `x` and its reflected image `r_j(x)`. But both variables and the function rule are hidden!

Your job is to find the rule.

Construct a domain to match the red trace.
Use Indep. Var. x to restrict `x` to the domain and make a Vary x button.
Reflect `x` to construct the dependent variable.
Adjust the function rule so that the dependent variable moves along the blue trace while you vary `x` along its domain.
Press New Case to try a different problem. Do as many problems as you need to get good at them.

What did you notice, and wonder, as you solved these problems?

The cases on this page are harder, but your job is the same: find the function rule so that `r_j(x)` follows the blue trace while you vary `x` along the red trace.

Construct a domain using the red trace, and restrict `x` to your domain.
Reflect `x` to construct the dependent variable, and adjust the function rule.
You’ve solved the case when your two variables move exactly along the two traces.
Practice on more cases until you are reasonably confident about your guesses.

Why was this page harder than page 1?

Make a drawing of your solution to a particularly interesting case. Show the traces, both variables, and the mirror line.

After your practice on pages 1 and 2, you’re ready to guess the location of the mirror ahead of time.

Make your guess by using the Line tool.
Construct the domain, restrict `x` to the domain, and reflect in your line.
Press the Vary x button to check your guess.

How close was your first guess? Did you get it exactly right?

To improve your skills, practice with several more cases. Follow the steps below for each new case:

Undo your reflection.
Press New Case.
Adjust your line for the new case.
Adjust your domain for the new case, and reflect in your line.
Vary x to see how well you did.

How did more practice help you improve your accuracy?

Describe your strategy for locating the mirror. What did you pay attention to as you adjusted its two points?

On this page you have another new tool.

Experiment to see if you can use both the Midpoint tool and the Line tool to make a more accurate guess about where the mirror should be.

Construct the domain, restrict `x` to the domain, reflect in your line, and vary `x` to check your guess.

How close was your first guess? Did you get it exactly right?

Do these next steps at least two times. As you do so, think about how to use the Midpoint and Line tools together to make the best possible guess.

Undo all the way back to when you used the Midpoint tool.
Press New Case.
Use the Midpoint and Line tools to make a guess for the new case.
Adjust your domain, reflect `x` in your guess, and check your result.

Describe your strategy for for using the Midpoint and Line tools to locate the mirror.

Why do you think this strategy works?

This page has a Midpoint tool and a Perpendicular tool.

As you did on previous pages, experiment to figure out how these two tools can help you guess the mirror correctly.

What strategy did you invent, using these two tools, to figure out the location of the mirror?

Explain in your own words why you think this strategy works.

5 Interlude

From I Love Lucy Season 4 Episode 27. Downloaded from https://www.youtube.com/watch?v=TNm5Dax56ck

How does this video relate to the reflect dance you did earlier?

6 Reflect Games

Each page of this sketch has a different game.
For each game play a few times at easier levels, and work your way up to level 5.
Once you start a game at one level, you must press Reset to change to a different level.

Loading...

Where is `r_j(x)?` Drag `y` to the spot, and press Check.

Where is `x?` Drag `z` to the spot, and press Check.

Where’s the mirror that relates `x` and `r_j(x)?` Drag `P` and `Q` to show your guess.

Given independent variable `x` and mirror `j`, describe how to find `r_j(x).`
Given mirror `j` and `r_j(x)`, describe how to find independent variable `x.`
Given independent variable `x` and `r_j(x)`, describe how to find mirror `j.`
How is this way of adjusting the mirror different from page 3?
For this game, what was the highest level at which you scored 8 hits in ten tries?
What methods did you invent to help you improve your score?

7 Reflect Dance 2

On the Floor

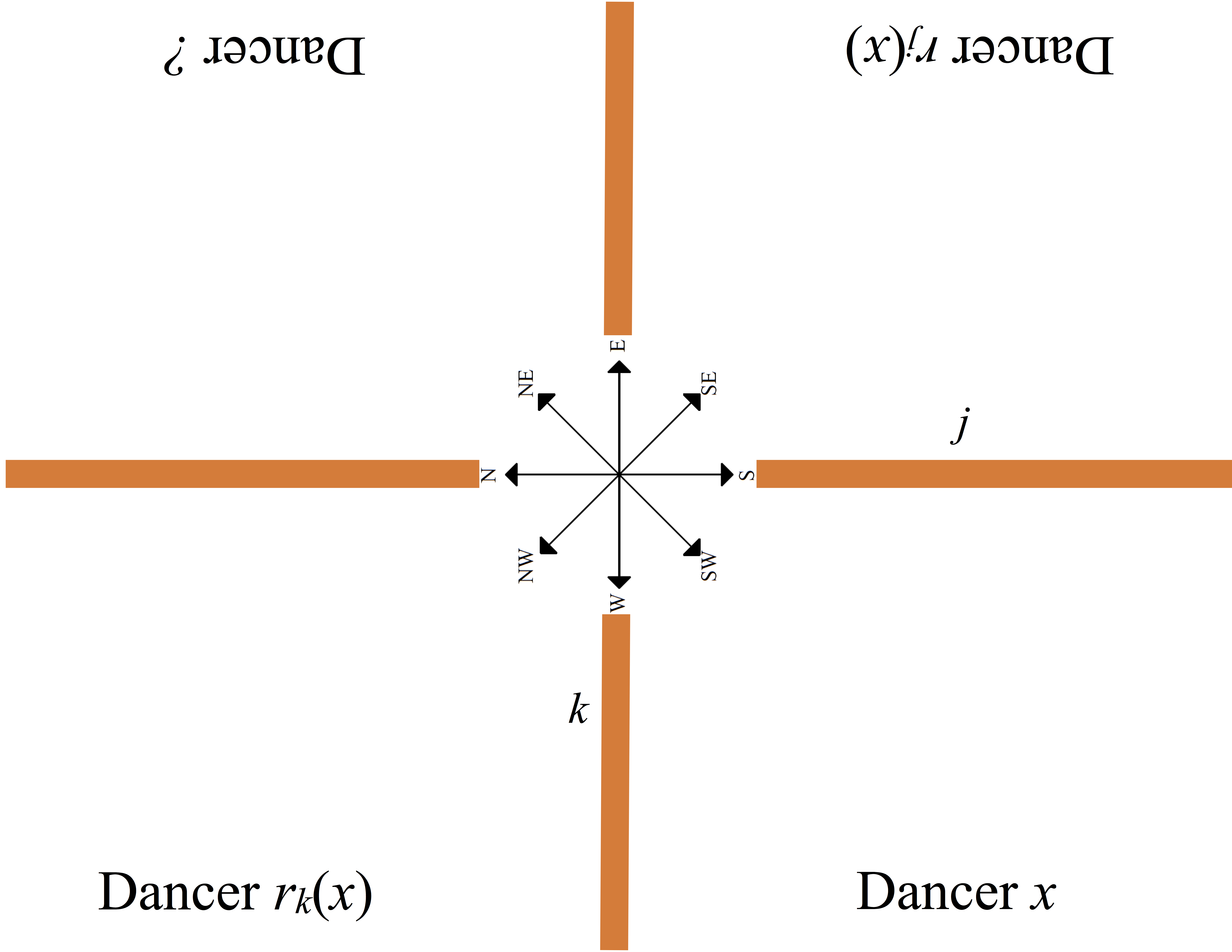
In a group of four or five students, tape a dance guide paper on the classroom floor to mark two perpendicular mirrors. Invent a reflect-family dance that uses both mirrors.

Dancer `x` is the independent variable and dancer `r_j(x)` is the reflected image, in mirror `j`, of `x`. Dancer `r_k(x)` is the reflected image in mirror `k` of `x`. Decide among yourselves how the fourth dancer should move. As you create and practice your dance, check to be sure the dancers are correctly positioned relative to the mirror.

As you choreograph and practice your dance, take turns so everyone in the group has a chance to be the independent dancer. When you’re ready to perform your dance, ask someone from another group to video your group dance.

As you created your dance, how did you decide the fourth dancer should move?

In what direction must each of the other dancers move when `x` moves north? south? east? west?

What else did you notice, and what did you wonder, about the reflect functions that connect your dancers to each other?

How could you use function notation to describe the fourth dancer?

On the Screen

Loading...

Hint Video:

Use this page to investigate reflections across perpendicular mirrors.

Construct a pair of angled mirrors and adjust them to make them perpendicular.
Label one mirror `j` and the other mirror `k`. Reflect `x` across each mirror.
Construct `r_j(r_k(x))` and `r_k(r_j(x)).`
Turn on tracing for your variables, and use the Style Widget to give them different colors.
Experiment by dragging `x` to make different shapes.
What do you notice about the speed and direction of the dependent variables when you dragged `x?`
What does the notation `r_k(r_j(x))` mean? How does the notation help you explain, in words, how the point is constructed?

When Juanita and Donte did this, Donte said, `“r_k(r_j(x))` is the same as `r_j(r_k(x))`.” Juanita said, “No it’s not!” They both had good reasons for their answers.

Help Donte explain why his answer is right.
Help Juanita explain why her answer is right.

Use this page to investigate reflections across angled mirrors that are not perpendicular.

Construct a pair of angled mirrors. Adjust them, but don’t make them perpendicular.
Label the mirrors and reflect `x` across each mirror.
Construct `r_j(r_k(x))` and `r_k(r_j(x)).`
Turn on tracing and drag `x` to make different shapes.
You can also try different mirror angles. (You should erase traces any time you change the angle.)

What do you think Juanita and Donte said to each other when they did this construction?

How would you explain to a classmate what is special about perpendicular mirrors?

Use this page to investigate reflections across parallel mirrors.

Construct parallel mirrors, adjust them so they’re vertical, and reflect `x` across each mirror.
Construct `r_j(r_k(x))` and `r_k(r_j(x)).`
Turn on tracing and drag `x` to make different shapes.
What do you notice about the shapes that `r_j(r_k(x))` and `r_k(r_j(x))` trace?
What do you notice about the locations of `x,` `r_j(r_k(x)),` and `r_k(r_j(x))?`
Put the mirrors closer together, or farther apart.
How does changing the distance between the mirrors affect the relative locations of `x` and `r_j(r_k(x))?`
Put the mirrors at a different angle, so they are not vertical.
How does changing the mirror angle affect the relative locations of `x` and `r_j(r_k(x))?`

Use this page to choreograph a dance using parallel mirrors.

Construct parallel mirrors and reflect `x` to make `r_j(x)` and `r_k(r_j(x))`
Give your variables different colors and turn on tracing.
Use the Free Style tool to choreograph a dance domain for `x.`
Use the Dance tool to make `x` dance along its domain.
If you like, add more parallel mirrors and more traced reflections.
You can take some of your variables out of the performance by turning off their tracing.
Draw a picture of the dance you choreographed. Label the mirrors and the variables in your drawing.

Use this page to choreograph a dance using angled mirrors.

Construct angled mirrors and decide what angle to use.
Reflect `x` to make `r_j(r_k(x)),` and `r_k(r_j(x)).`
Give your variables different colors and turn on tracing.
Use the Free Style tool to choreograph a dance domain for `x.`
Use the Dance tool to make `x` dance along its domain.
Adjust your choreography to your liking. You can add more mirrors and more reflections, you can take some variables out of the performance by turning off their tracing, and you can adjust your domain by dragging the domain points.
Draw a picture of the dance you choreographed. Label the mirrors and the variables in your drawing.

Professional Dancers

NY Times 25 October 2016 Suzanne Farrell Ballet at Kennedy Center

8 Dependent Dance Challenge

Until now, you’ve mostly been the independent variable (the penguin): either you were free to move around the plane, or you could move along a restricted domain. But in this challenge, you are the dependent variable (the frog), and your challenge is to follow the function rule as the penguin moves around her restricted domain.

To move correctly, you have to always be in the correct location across the mirror from the penguin. Fortunately you have a reflection segment to help you. When the penguin is in the center of the white circle, you are in the correct location for the function rule.

The hard part comes when the penguin starts moving: because you’re the dependent variable, you have to move to keep the white circle centered on the independent variable.

Before you start the game, practice moving the frog so the circle and cross-hairs move around the border of the polygon, because that's the path that the penguin will dance.

When you’re ready to play, move the frog so the cross-hairs are over the penguin. Then press the Countdown button and get ready to move the frog. When the countdown ends and the independent variable starts moving, you have to move the dependent variable to always be the reflected image.

Both the polygon and the trace will change color, from red to green, when you’re in the right place.

Loading...

What did you notice, and wonder, as you practiced the dance on page 1?
Did you get better as you practiced? Could you do the dance at a more difficult level and still keep the colors green?

Once you master this dance, go to page 2 for a slightly harder challenge.

Page 2 has another challenge using a different polygon and mirror.

Is the dance on pages 2 easier (because of your practice on page 1) or harder? Explain.
Having done physical dances and virtual dances, is it easier being the independent variable or the dependent variable? Why?

9 Accomplishments

To prepare for the summary discussion, use the prompts below to record your accomplishments and “reflections.” (Sorry: bad pun ☹️)

What did you observe and learn about how the Reflect function family behaves?
Specifically, what did you learn about how `r(x)` moves relative to `x?`
Describe one or two new skills you developed.
List one or two new terms you learned, and explain the term(s) in your own words.
Describe one or two things you learned about double reflections (using two mirrors).
Which was your favorite activity of the lesson? Why?
What was your least favorite activity of the lesson? Why?
Describe an example of a reflect function, not already mentioned in this lesson, that you can observe in your school or in your neighborhood.

The Fine Print

Requirements:

These activities require web access using a browser that supports HTML5 and JavaScript. (That means almost any current browser.) No purchase is required, and there’s no advertising anywhere.

Release Information

[an error occurred while processing this directive]

Update History:

Record every major revision, in reverse chronological order

23 Apr 2020: Added downloadable worksheet, Reset buttons, and Accomplishments section.
04 Mar 2018: Converted to new lesson format.
06 Mar 2017: Fixed a bug on page 5 where the x tool didn’t work.
16 May 2016: Updated websketch page 8 to eliminate tracing, which was confusing.
31 Oct 2015: Updated this page to the website format.