
1 Introduction 8:02
Constructive Proofs: Use Web Sketchpad to Prove SSS
Scott Steketee, 21st Century Partnership for STEM Education, stek@21pstem.org
Daniel Scher, McGraw-Hill Education, daniel.scher@mheducation.com
Donovan Hayes, Hill-Freedman World Academy, Philadelphia, dhayes@philasd.org
2 Benefits of a Transformation Approach8:04
🔵
🔵
🔵
🔵
🔵
🔵
3 The Problem with Congruence8:08
The traditional approach to congruence is fraught with difficulties, leaving triangle congruence properties based on assumptions instead of proofs. A transformation approach overcomes those difficulties, opening a path for students to confront and solve the challenge of proving SSS as a theorem.
4 Function Dances
3a A Simple Reflection Dance8:18
Work with a partner to perform two short reflect dances, moving as if there is a mirror between you. To locate the mirror, put a piece of tape on the floor, with a dance guide paper in the middle of the mirror like this:

For the first dance, flip a coin to identify one person as the independent dancer and the other as the dependent dancer. You will switch roles for the second dance.
Independent Dancer: Always look at your partner, and take steps according to the directions below. As you dance, you can do any other body movement that’s both safe and simple enough that your partner can mirror it. Start one step back from the middle of the mirror.
Dependent Dancer: Mirror your partner’s movements, staying exactly across the mirror from your partner and the same distance away from the mirror.
First Dance:- 4 steps south
- 3 steps west
- 3 steps northeast
- 2 steps north
✏️ Draw a diagram to show the path that each of you followed.
✏️ Describe the relative directions you moved in each part of the dance.
Second Dance: (after switching roles)Begin with the three-part dance routine below and finish by improvising your own dance pattern. If possible, ask a classmate to video your dance.
- 3 steps southwest
- 2 steps east
- 3 steps northwest
- Improvise and record the rest of your dance routine
✏️ When did you both move in the same direction? When did you move in opposite directions?
2b A Student Mini-project: Transformation Dances8:21
This dance was part of a student project that required each dance team to use all of the transformations they had been studying.
5 A Line with Five Identities8:35
There are five ways you can think about this line:
- It’s the locus of all the fixed points of the function that takes `x` to `r(x)`.
- It’s the mirror line that defines the reflect function that takes `x` to `r(x)`.
- It’s the locus of points that are the same distance from `x` as they are from `r(x)`.
- It’s the perpendicular bisector of the segment between `x` and `r(x)`.
- It’s the line constructed using the intersections of the two circles defined by points `x` and `r(x)`.
Use the tools to construct and/or trace all of these in turn, each on its own page. The tools include Hide/Show buttons you can use to hide or show each way of constructing or tracing this line.
In your own words, describe something that's interesting or important about each of these five—five lines that are all the same, but also different, each in its own way!
Technology Tips:
Web Sketchpad (WSP) is our dynamic geometry platform. Each WSP activity provides only a small number of tools, simplifying the user interface and encouraging productive exploration.
When you tap to activate a tool, the entire construction appears, ready for you to place its glowing objects where you want them, or to match them to existing objects in the sketch.
6 Summary and Discussion8:43
Setting the Stage for SSS
To set the stage for our constructive proof of the SSS Theorem, we’ve:
🔵
🔵
🔵
🔵
Big Mathematical Ideas
🔵
🔵
🔵
🔵
🔵
🔵
7 Patty Paper Reflection8:53
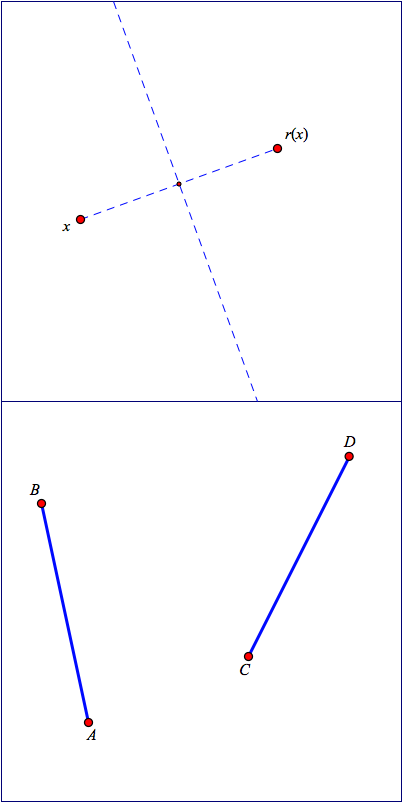
Click the image on the left to print it full size, or get a copy from your teacher. The top printed diagram shows `x`, `r(x)`, and the constructed line of fixed points. Trace points `x` and `r(x)` onto a piece of patty paper. Fold the patty paper so that `x` lies on top of `r(x)`.
✏️ How does the patty-paper fold line relate to the fixed points of the reflect function connecting `x` and `r(x)`?
Use the bottom printed diagram to trace `\overline{AB}` and `\overline{CD}` on a new sheet of patty paper. Fold the patty paper to reflect `A` onto `C`, trace the reflected location of `\overline{AB}`, and label the reflected endpoints `A'` and `B'`.
Unfold your paper. Then make a new fold to put `B'` on top of `D`.
✏️ What do you notice? What do you wonder?
8 Mirror, Mirror8:56
On each page of this activity you’ll try to construct multiple reflect functions to produce the exact same result as other transformations. The functions you'll try to construct this way include a rotate function (page 2), a translate function (page 3), a glide reflection (page 4), and a dilate function (page 5). (Hint: all of these except one are possible.)
9 Prove the Segment Congruence Theorem9:08
Using the traditional approach to congruence (defining congruence in terms of equal measures), the distinction between two segments having equal lengths and two segments being congruent was meaningless. Students found the distinction silly: "Of course two segments of equal length are congruent, because equal length and congruent mean the same thing!"
With a transformation approach, the distinction becomes meaningful. To claim that two segments are congruent, you have to do more than just measure them: you have to show that one can be transformed so its image is superposed on the other.
Our ultimate goal will be to prove the SSS Theorem, but as with so many difficult problems, it's very useful to do a simpler problem first. If we can prove the Segment Congruence Theorem, you'll find that proving the SSS Theorem is a piece of cake.
Construct and prove the Segment Congruence Theorem: Given `AB = CD`, the two segments `overline(AB)` and `overline(CD)` are congruent.
Remember that congruent figures are figures that can be superposed using isometries,transformations that preserve distance and that any other isometryrotation, translation, or glide reflection can be produced by a composition of reflections.
You can rephrase the task: Given `AB = CD`, use reflections to superpose an image of `overline(AB)` on `overline(CD)`.
Because this is a proof task, you must be able to explain why each step of your construction works.
On page 1 you will develop your strategy for superposing an image of `overline(AB)` on `overline(CD)`. The given fact of the proof `(AB = CD)` has already been applied, so you just need to figure out how to construct the transformations.
How many perpendicular bisectors, and how many reflections, do you need to superpose your segments?
On page 2 the given fact has not yet been applied. You need to figure out when, and why, you need to use the given fact to make your construction work correctly.
As you do your construction, when is it most convincing, or most logical, to apply the given fact?
On page 3, as you do each step of the construction, describe that step and explain why it works the way it does.
Organize your page 3 descriptions and explanations in a clear logical way (paragraph, two-column format, or other format specified by your teacher).
By describing what you did, and explaining why it works, you have proved the Segment Congruence Theorem.
Video hints are not yet available.
10 Prove the SSS Theorem
Construct and prove the SSS Theorem: Given `triABC` and `triDEF` with `AB = DE`, `BC = EF`, and `CA = FD`, the two triangles are congruent.
Remember that congruent figures are figures that can be superposed using isometries, and that any isometry can be produced by a composition of reflections.
You can rephrase the task: Given `triABC` and `triDEF` with `AB = DE`, `BC = EF`, and `CA = FD`, use reflections to superpose an image of `triABC` on `triDEF`.
On page 1 you will develop your strategy for superposing an image of `triABC` on `triDEF`. The givens of the proof `(AB = DE`, `BC = EF`, and `CA = FD)` have already been applied, so you just need to figure out how to construct the transformations.
How many perpendicular bisectors, and how many reflections, do you need to superpose your triangles?
On page 2 the givens have not yet been applied. You need to figure out when, and why, you need to use the three given facts to make your construction work correctly.
As you do your construction, when is it most convincing, or most logical, to apply each given fact?
On page 3, as you do each step of the construction, describe that step and explain why it works the way it does.
Organize your page 3 descriptions and explanations in a clear logical way (paragraph, two-column format, or other format specified by your teacher).
By describing what you did, and explaining why it works, you have proved the Side-Side-Side Triangle Congruence Theorem.
Video hints: Page 1
11 Summary and Discussion9:15
What we’ve done:
- Adopted a transformation approach to solve important problems with congruence
- Connected transformations to function concepts (independent/dependent, rate of change, notation)
- Used our bodies as variables following a function rule
- Used patty paper to experiment with superposition as the criterion for congruence
- Used WSP to establish the important role of perpendicular bisectors and the Perpendicular Bisector Theorem
- Used WSP to experiment with superposing two congruent triangles
- Used WSP, with history icons, to prove the Segment Congruence Theorem
- Left the SSS Theorem as an exercise for participants
12 Resources
WSP Tool Library: geometricfunctions.org/fc/tools/
The Fine Print
Requirements:
These activities require web access using a browser that supports HTML5 and JavaScript. (That means almost any current browser.) No purchase is required, and there’s no advertising anywhere.
Release Information
[an error occurred while processing this directive]Update History:
Record every major revision, in reverse chronological order
24 Jan 2018: Created this lesson template.

