Introducing Web Sketchpad

1 WSP Provides a Simple, Intuitive Interface

Simple:

No menus.
No unneeded tools.
The only dialog boxes are the calculator/function editor and the number pad.
Widgets allow you to change the style, tracing, labeling, and other properties of objects.
Many sketches incorporate silent hint videos.

Intuitive:

Drag an object to move it. Most objects can be dragged, but some cannot.
Tap a button to perform its action.
With an active widget, tap an object to apply the widget's action.
With an active tool, tap an object to match it to the tool’s current given.

Loading...

Hint Videos:

Source: This activity comes from the Identify Functions lesson.

Please post your questions, comments, and suggestions here: sineofthetimes.org/nctm-2021-wsp-workshop/

2 WSP Uses Self-Scaffolding Tools Featuring Up-Front Tool Preview

Using tools in Web Sketchpad:

Everything the tool will produce is immediately visible, with the first object to be matched already glowing.
Tap to position or match the glowing object, or...
..drag any given object, whether it’s glowing or not.
Until the tool is finished, you can drag any already-matched given object to reposition or rematch it.
To preview the results of any tool, choose it and then tap the green OK button. After checking out the tool’s effect, tap the Undo arrow to undo.

Because all tools work this same way, it’s easy for you and your students to figure out how to use them with no need for additional documentation, explanation, or demonstration.

Use the tools in the sketch below to construct a triangle and its orthocenter. As you work, practice the different ways of placing the given objects of the tools.

[This websketch was created using the WSP Tool Library. Watch this video to see how to create it yourself. After downloading it, you can distribute it to your students, tell them to upload it to the Tool Library, do the construction, and submit their downloaded sketch to you. You can then show the collected websketches in the WSP Sketch Viewer for a class discussion.]

Loading...

3 WSP Tailors Tools to the Task

With Web Sketchpad, teachers and curriculum designers can decide on a task and create a sketch that contains carefully-chosen tools specific to the proposed task.

Each page of the websketch below contains a small set of tools that can be used to construct a rhombus.

On each page, construct a rhombus using the available tools.

Notice how each collection of tools focuses students’ attention on different properties of a rhombus.

Loading...

4 WSP Integrates the Function Concept into Students’ Geometric Thinking

This section has three pairs of tasks, all about how functions connect geometry and algebra. In the first pair you construct Dynagraphs, in the second you compare Dynagraphs with Cartesian graphs, and in the third you consider possible advantages of combining the two forms of graphs.

As you engage with these tasks, please keep in mind three kinds of connections that are critical for good mathematical learning:

Mathematical connections abound throughout mathematics. In this tasks, we'll leverage WSP to stress the connection between geometric functions (transformations) that operate on points and algebraic functions that operate on numbers.
Pedagogical connections allow us to improve students’ learning by engaging them in constructing, noticing, wondering, discussing, and reflecting.
Cognitive science connections suggests that we treat seriously the research that reveals how conceptual understanding in mathematics arises from mind-body connections called conceptual metaphors.

Presentation URL:
geometricfunctions.org/fc/present/nctm-apr-2021/?user=teacher

(The “?user=teacher” part shows the Ⓣ teacher-notes buttons, which provide helpful or interesting information relevant to the context.)

a. Transform in LineLand

In this activity you can make some fascinating discoveries linking transformations with the domain restricted to a line to important algebraic operations. Give it a try, and record your discoveries.

Loading...

Hint Video:

Construct `D_(0,s)(x)`, restricting `x` to a line.
Measure the coordinates of the points.
As you vary `x`, how are the values of the independent and dependent variables related?
Try several values of the scale factor. How does it affect the relationship between `x` and `D_(0,s)(x)?`
When you finish, go to page 2 to work with the Translate function.

Construct `T_(0\rightarrowv)(x)`, restricting both `x` and `v` to a line.
Measure the coordinates of the points.
As you vary `x`, how are the values of `x` and `T_(0\rightarrowv)(x)` related?
When you finish, go to page 3 to combine a Dilate function and a Translate function.

Construct `T_(0\rightarrowv)(D_(0,s)(x))`, restricting `x` to a line.
Measure the coordinates of the points.
As you vary `x`, how are the values of `x` and `T_(0\rightarrowv)(D_(0,s)(x))` related?

Use the to set both blue points to use “Short” function notation instead of “Full” function notation.
Can you write an algebraic formula that gives the value of `T(D(x))` in terms of `x`, `s`, and `v?`

Source: This activity is adapted from the lesson From Flatland to Numberland.

Next, you’ll use an axis tool by adding numbers and tick marks, and you’ll put the dependent variable on a second parallel axis to make your observations easier.

b. Construct a Dynagraph

In the previous task, you discovered that restricting a dilate function to the number line produces multiplication, and restricting translation to the number line produces addition.

In this task, we'll actually construct a Dynagraph.

Loading...

Construct `D(x)` with `x` restricted to a number line.
As you vary `x`, how is the value of `D(x)` related to `x` and `s?` Write both a description and a formula.
Transfer both the origin and `D(x)` downward, and construct a new number line matching its origin to the transferred origin.
Vary `x` to make sure the two `D(x)` variables always match. Then use the Visibility Widget to hide the dashed lines.
Translate the new `D(x)` on its number line.
As you vary `x`, how is the value of `T(D(x))` related to `D(x)` and `v?` Write both a description and a formula.
Connect `x` on the top number line to `T(D(x))` on the bottom line, and use the Trace Widget to turn tracing on for the connecting line.
When you vary `x,` what do you notice about the traces of the connecting line?
Try different values of `s` and `v.` How can you tell from the traces whether `T(D(x))` is moving faster or slower than `x?` Draw pictures of your traces to explain your answer.
How can you tell from the traces whether `T(D(x))` is moving in the same direction or the opposite direction as `x?` Draw pictures to support your explanation.
Use pages 2 and 3 to construct more functions, and to show how different values of `s` and `v` affect the shape of the traces.
Write a formula for the value of `T(D(x))` in terms of `x, s,` and `v.` Check your formula by varying `x` and adjusting `s` and `v.`

Source: This activity comes from the lesson Construct a Dynagraph.

Since you already know that dilation corresponds to multiplication, and translation to addition, what kind of algebraic function is created by the composition `T(D(x))?`

Next, let's compare two WODB student activities, one based on Cartesian graphs and one based on Dynagraphs.

Take a look at both activities, and for each activity predict several things that students might say to explain why one is different from the other three.

c. Which One Doesn’t Belong? (Static)

Which graph doesn't belong with the other three?

For each graph, find a way that it’s different from the others.

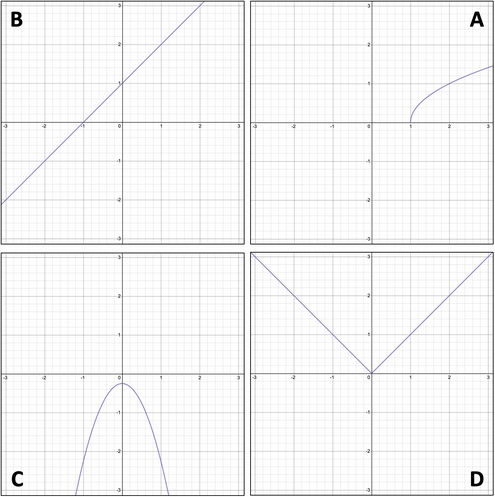
Why does graph A not belong with the others?
Why does graph B not belong with the others?
Why does graph C not belong with the others?
Why does graph D not belong with the others?
Draw your own graph E that doesn't belong with the other four.

d. Which One Doesn’t Belong? (Dynamic)

For each function below, drag independent variable `x` to see how the dependent variable moves.

Which function doesn't belong with the other three?

Loading...

For each function, find a way that its behavior is different from the others.

Why does function `f` not behave like the others?
Why does function `g` not behave like the others?
Why does function `h` not behave like the others?
Why does function `k` not behave like the others?
Imagine function `q` that doesn't belong with `f, g, h, or k.` How does it behave?

Summary Questions:

What function features or behaviors did you particularly notice in the Cartesian (static) version?
What function features or behaviors did you particularly notice in the Dynagraph (dynamic) version?
What insights do you predict students might develop by doing the static version?
What insights do you predict students might develop by doing the dynamic version?

Please post your answers and comments here: sineofthetimes.org/nctm-2021-wsp-workshop/

e. Connect the Dynagraph and the Cartesian Graph

In this activity and the next you will consider two possible ways to connect the Dynagraph and Cartesian graph of the samne function in a single window. This activity shows them as two separate (but connected) graphs.

Drag either either independent variable (`x`) to observe the function’s behavior.
Experiment with the controls in the right panel to see what they do.
After you show the Cartesian point, use the Trace Widget to trace it.
Every page of the websketch shows a different function. To edit the function, double-tap it.

Loading...

Hint Videos:

Connections

Cartesian Point
`(x, f(x))`

Variable

Axes

Min:
Max:

Angle Units
Degrees
Radians

Describe an aspect of function behavior that’s easier to understand using the DynaGraph.
Describe a different aspect of function behavior that’s easier to understand using the Cartesian Graph.
Describe something new that you figured out by seeing the same function in both forms.

f. From DynaGraph to Cartesian Graph

This activity shows the two forms as a single graph in which you can rotate the dependent variable's axis to make it either parallel or perpendicular to the independent variable's axis.

Drag `x` to see how `f(x)` behaves.
Drag the white point at 1 on the output axis to rotate it.
Try each of the buttons to see what they do.
Use the Trace Widget to trace the connector as you vary `x.`
Double-tap the function to enter a function of your own.

Loading...

Hint Videos:

Describe an aspect of function behavior that’s easier to understand using the DynaGraph.
Describe a different aspect of function behavior that’s easier to understand using the Cartesian Graph.
Describe something new that you figured out by seeing the same function in both DynaGraph and Cartesian Graph form.

Summary Questions:

What advantages do you see to the first websketch (activity 4e)?
What advantages do you see to the second websketch (activity 4f)?
What overall benefit might there be in having students use both representations on a regular basis?.

Please post your answers and comments here: sineofthetimes.org/nctm-2021-wsp-workshop/

5 WSP Enables a Transformation Approach to Geometric Constructions and Congruence

5a Proofs Without Words

Proofs Without Words is a series of books from the American Mathematical Society containing “figures or diagrams that help the reader see why a particular mathematical statement may be true and how one could begin to go about proving it.” Though the figures themselves are not technically proofs, they are elegant graphical illustrations of the important mathematical truths whose proofs they suggest.

Particularly for transformational proofs, such figures can be clearer and more convincing in a dynamic environment that supports animating the transformation. The example below, created using the WSP Tool Library, demonstrates the Triangle Sum Theorem and suggests its proof.

The finished dynamic figure is on page 1; page 2 is a blank page that you (and your students) can use to recreate the dynamic “proof without words” on page 1.

[As a side note, the technique used in this websketch, a half-turn rotation about the midpoint of a segment, can similarly be used on a traversal segment between parallel lines to prove the Alternate Interior Angle Theorem, which is the basis for the usual non-transformational proof of the Triangle Sum Theorem.]

Loading...

Use page 2 of the sketch to recreate the animation on page 1, using your own visual styles for the geometric objects.
You can use the Style Widget to modify the colors and styles of objects on page 1 to make it a more effective presentation.
You can even download the sketch, using the Utility menu, and edit it using the using the WSP Tool Library.

5b Quadrilateral Definitions

The different families of quadrilaterals are generally defined in terms of lengths of sides and measurements of angles. But here and here are strong arguments for using symmetry to define special quadrilaterals. The symmetry-based definitions have an advantage in formulating proofs, since the symmetry that defines a special quadrilateral can be used to prove other facts about it.

Loading...

Construct a quadrilateral with two lines of reflection symmetry. The vertices should lie on the lines of symmetry.

Construct two perpendicular lines. These will be the lines of reflection symmetry for your quadrilateral.
Construct a point on each line, and reflect each constructed point across the other line (that is, across the line that it is NOT on).
Use the resulting four points to construct a quadrilateral.
Drag the vertices to see what shapes are possible.
What special kind of quadrilateral did you just construct?

Construct a quadrilateral with two lines of reflection symmetry. The lines of symmetry should pass through the midpoints of the sides.

Construct two perpendicular lines. These will be the lines of reflection symmetry for your quadrilateral.
Construct a point that is not on either line. Reflect it across one line.
You now have two points. Reflect each of them across the other line.
Use the resulting four points to construct a quadrilateral.
What special kind of quadrilateral did you just construct?

Construct a quadrilateral with a single line of reflection symmetry. The line of symmetry should pass through two opposite vertices.

Construct a single line of reflection symmetry for your quadrilateral.
You can use the points that determine the line as the two opposite vertices, with the line as their diagonal.
Construct another point not on the line, and reflect it across the line.
Use the four points to construct a quadrilateral.
What special kind of quadrilateral did you just construct?

Is there a special quadrilateral that has one line of symmetry that does not pass through any vertex? If so, how can you construct it? What special kind of quadrilateral is it?

How does this approach to categorizing special quadrilaterals relate to your earlier work with finding multiple ways to construct a rhombus?

5c The Problem with Congruence

The traditional approach to congruence is fraught with difficulties, leaving triangle congruence properties based on assumptions instead of proofs. A transformation approach overcomes those difficulties, opening a path for students to confront and solve the challenge of proving SSS as a theorem.

Loading...

5d Mystery Transformations

Put the image of `triangleABC` into superposition with `\triangleDEF.` Each page shows a different function family—but which one?

You can use handedness to help you decide.

When you think you know the function family, use the shortcut you invented for that family, either before or after actually transforming `triABC.`

Loading...

Summary Questions:

One of these pages did not show congruence. Which page was it, and what did it show instead?
Did you use handedness to help figure out which function to use? If so, how did it help you?
Did you use any shortcuts to help you superpose triangles? If so, what was your favorite shortcut?

Please post your answers and comments here: sineofthetimes.org/nctm-2021-wsp-workshop/

Source: This activity comes from the Mystery Transformations lesson.

5e Prove SSS: No Longer a Postulate

The transformation-based proof of the Side-Side-Side Theorem relies on several definitions and facts.

Definition: An isometry is a transformation on the plane that preserves distances.
Definition: Two figures are congruent if and only if you can use an isometry to superpose an image of the first figure on the second.
Fact: Every isometry is equivalent to the composition of 1, 2, or 3 reflections.
Fact: The reflection that superposes the image of point `A` on point `B` is the perpendicular bisector of `\overline(AB).`
Fact: Points `A` and `B` are equally distant from point `C` if and only if `C` lies on the perpendicular bisector of `\overline(AB).` (Perpendicular Bisector Theorem and Converse)

To prepare for proving SSS, we’ll use the sketch below to construct and prove the Segment Congruence Theorem:

`\overline(AB) cong \overline(CD)` if and only if `AB = CD.`

Then you can use this link for the lesson in which you construct and prove the Side-Side-Side Theorem.

Loading...

6 WSP Supports Distance Learning/Virtual Classrooms

Teachers and students can use Web Sketchpad to construct, investigate, collaborate, and prove in both virtual and in-person environments. It provides exceptional support for good pedagogical processes.

Specifically, Web Sketchpad:

enables teachers and students to construct, investigate, collaborate, and prove in both virtual and in-person environments,
integrates tightly into web pages,
supports and reinforces good pedagogical practices even in virtual classrooms,
enables noticing and wondering (Construct a Rhombus, Which One Doesn’t Belong),
promotes the five practices (WSP Viewer),
encourages student agency (intuitive interface, self-documenting tools),
supports per-task tailoring of tools (creating instrumented fields of promoted action), and
leverages cognitive-science research (embodied cognition, concreteness fading).

Web Sketchpad remains under active development, and we are eager to further develop and extend the lessons on the Forging Connections website (created with National Science Foundation support under IUSE award 1712280).

Here’s are some of the ways you can use WSP effectively with your own students:

You can assign, and your students can use, many of the lessons from the Forging Connections website.. (Full disclosure: a number of the lessons are still in draft, so check a lesson before assigning it to your students.)
On this page, you and your students can view WSP video tutorials and access the WSP Tool Library and the WSP Sketch Viewer
You can assign constructions for students to complete using the WSP Tool Library.
Using the Tool Library, students can download their completed constructions and transmit them to you.
You can then load these student submissions into the WSP Sketch Viewer for the class to review and discuss, either in-person or in a Zoom meeting.
You can use the WSP Tool Library to create an activity for your students. You can either post it as a web page or distribute it to students via email, Google Classroom, or similar mechanisms.
You can use some of the many additonal WSP activities (for elementary through high school) that reside on the sineofthetimes.org blog. This site features a compendium of elementary WSP activities.
You can use WSP activities on the NCTM Illuminations site, including the highly regarded Bunny Times multiplication app.
For non-commercial purposes only, you are free to use any of the materials in this list, and any of the materials on this workshop web page.

.

7 WSP Is a Worthy Successor to GSP and Other Dynamic Geometry Software

With its support for both virtual and in-person math classes and its tight integration into web pages, WSP is truly a worthy successor to The Geometer's Sketchpad and other dynamic mathematics software.

The Geometer's Sketchpad can be used as an authoring environment for WSP websketches.
The Web Sketchpad Exporter turns GSP sketches into WSP websketches or into full WSP-based web pages.
Web Sketchpad has near-complete support for GSP Sketches.
Web Sketchpad’s user interface is exceptionally clean and simple to learn and use.
Web Sketchpad’s tools are self-documenting and easy to use.
It’s easy for the sketch author to tailor the available tools to the task.
WSP brings new features that are unavailable in other dynamic mathematics software, including Function Notation, Glide Reflections, and Drag Merging.

8 WSP Continues to Move Forward in Support of Students and Teachers

McGraw-Hill Education continues to support new-feature development, most recently including an improved tool interface, enabling different tools on different pages of a sketch, adding drag merging, and improving students’ ability to add explanatory text to their constructions.

The NSF has funded the Forging Connections project in which we’ve developed lessons for preservice secondary math teachers. (The student view of these lessons is appropriate for use with high school students, and many of the activities you used in this workshop come from the Forging Connections project lessons.)

We look forward to further advances both in WSP itself and in the availability of high-quality WSP activities from early grades through teacher-preparation programs.

All of the materials in this workshop video, on this presentation site, on the Forging Connections site, and on the sineofthetimes.org blog are freely available for non-commercial use, as is Web Sketchpad itself.

We welcome your questions, comments, and suggestions. Please post them here: sineofthetimes.org/nctm-2021-wsp-workshop/

A New Model for Creating and Exploring Dynamic Mathematics

NCTM Annual Meeting (April 2021)

What’s Different about Web Sketchpad, and Why Does It Matter?

Simple:

Intuitive:

Using tools in Web Sketchpad: