AMTE: Resources for Online Learning
February 20, 2021
Overview
This presentation is based on work supported by the National Science Foundation under NCSU IUSE award 1712280. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the presenters and do not necessarily reflect the views of the National Science Foundation.
| Project Team | Advisors |
|---|---|
| Karen Hollebrands, North Carolina State University | Al Cuoco, Education Development Center |
| Allison McCulloch, UNC-Charlotte | Roger Howe, Yale University & Texas A&M |
| Scott Steketee, 21PSTEM | Rachael Kenney, Purdue University |
| Daniel Scher, 21PSTEM | Brian Lawler, Kennesaw University |
| Ricardo Nemirovsky, Manchester Metropolitan University | |
| Joshua Taton, Philadelphia School District |
Project Goals
- Strengthen the mathematical background of future mathematics teachers, using a geometric approach to functions.
- Lead with geometry rather than algebra, grounding teachers’ understanding in a visual, sensorimotor, and embodied approach to mathematics.
- Capitalize on the ability of Web Sketchpad to design one-of-a-kind mathematical tools tailored to the needs of each particular lesson.
- Focus on student thinking and pedagogy through discussions of student interview videos and modeling the pedagogy that teachers will bring to their classroom.
Guiding Principles
- Activities build on preservice teachers’ current understandings.
- Mathematical ideas that unify and connect different aspects of mathematics are the focus.
- Technology is used to emphasize visual representations of mathematics and allow pre-service teachers to physically interact with mathematical objects through dragging.
- Technology provides customized tools so as to not over-constrain their work or distract them from the mathematics.
- Pre-service teachers experience the use of pedagogical strategies they are expected to implement in middle and high school classrooms.
- Pre-service teachers observe middle and high school students engaged in technology-based tasks that are of high-cognitive demand.
1 Which One Doesn’t Belong? (Static)
Which graph doesn't belong with the other three?
For each graph, find a way that it’s different from the others.
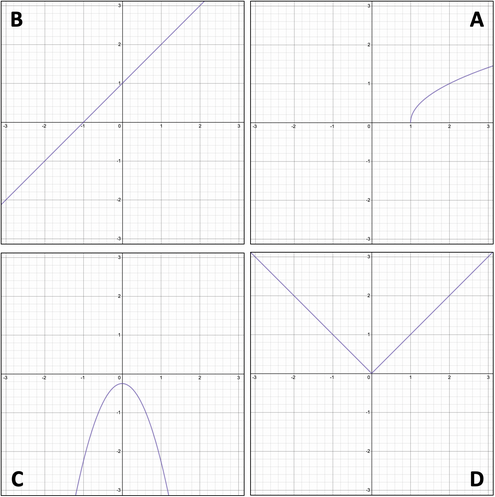
- Why does graph A not belong with the others?
- Why does graph B not belong with the others?
- Why does graph C not belong with the others?
- Why does graph D not belong with the others?
- Draw your own graph E that doesn't belong with the other four.
2 Which One Doesn’t Belong? (Dynamic)
For each function below, drag independent variable `x` to see how the dependent variable moves.
Which function doesn't belong with the other three?
For each function, find a way that its behavior is different from the others.
- Why does function `f` not behave like the others?
- Why does function `g` not behave like the others?
- Why does function `h` not behave like the others?
- Why does function `k` not behave like the others?
- Imagine function `q` that doesn't belong with `f, g, h, or k.` How does it behave?
3 Which One Doesn’t Belong? (Dynamic)
For each function below, press Vary `x` to see how the dependent variable moves.
You can also drag `x` to observe the function’s behavior.
Which function doesn't behave like the other three?
For each function, describe how it is different from the others.
- Why does function `f` not behave like the others?
- Why does function `g` not behave like the others?
- Why does function `h` not behave like the others?
- Why does function `k` not behave like the others?
- In this activity you used a button to vary `x.` Describe a difference in behavior that was easier to notice using the button.
- Describe a difference in behavior that was easier to notice by draging `x` yourself instead of pushing a button.
4 Connected Graphs
By using both a DynaGraph and a Cartesian Graph of a function, you can get a clearer idea of how the function actually behaves. This websketch connects the two graphs to help you see how they work together.
- Drag either either independent variable (`x`) to observe the function’s behavior.
- Experiment with the controls in the right panel to see what they do.
- Pages 2 and 3 of the sketch show different functions.
- You can edit any function by double-tapping it.
Tips for Using this Websketch
- Double-click the function to edit it.
- Use the Trace Widget to trace the path of the intersection `(x, f(x)).` (If you don’t see the Trace Widget, press the Widgets button.
- The Cartesian axes will be off-screen if Min and Max are both positive or both negative.
As you explore a function in both DynaGraph and Cartesian Graph forms, here are some questions for you to think about and to discuss with your classmates or your teacher.
- Describe an aspect of function behavior that’s easier to understand using the DynaGraph.
- Describe a different aspect of function behavior that’s easier to understand using the Cartesian Graph.
- Describe something new that you figured out by seeing the same function in both DynaGraph and Cartesian Graph form.
5 From DynaGraph to Cartesian Graph
Drag `x` to see how `f(x)` behaves.
Drag the white point at 1 on the output axis to rotate it.
Try each of the buttons to see what they do.
Use the Trace Widget to trace the connector as you vary `x.`
Double-tap the function to enter a function of your own.
Here are some questions for you to think about and to discuss with your classmates or your teacher.
- Describe an aspect of function behavior that’s easier to understand using the DynaGraph.
- Describe a different aspect of function behavior that’s easier to understand using the Cartesian Graph.
- Describe something new that you figured out by seeing the same function in both DynaGraph and Cartesian Graph form.
The Fine Print
Requirements:
These activities require web access using a browser that supports HTML5 and JavaScript. (That means almost any current browser.) No purchase is required, and there’s no advertising anywhere.
Release Information
[an error occurred while processing this directive]Update History:
Record every major revision, in reverse chronological order
This web site is based in part upon work supported by the National Science Foundation under NCSU IUSE award 1712280 (July 2017 through December 2020) and KCP Technologies DRK-12 award ID 0918733 (September 2009 through August 2013). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
We are deeply grateful to McGraw-Hill Education
for making Web Sketchpad available for these lessons.
Template by templatemo.com.
Nav by Chris Spooner, line25.com