This paper describes an approach to learning function concepts that uses innovative technology to engage students in constructing and manipulating functions—in the form of geometric transformations on the plane—and extending these sensorimotor experiences to help them make sense of linear functions and their Cartesian graphs.

This paper supports the authors’ presentation in the ICME-13 Topic Study Group 13 on Secondary Geometry. An extended version will be published in the Conference Proceedings, but this online paper has an added feature: Most of the figures are interactive, allowing you, dear reader, to experiment with the constructions yourself.

Each interactive figure includes a ‘Try it yourself’ button that you can use to show or hide the corresponding interactive websketch. The interactive websketches are accompanied by directions for use and by a link to the full activity, and the websketches with tools have a button for showing construction tips and links to short videos illustrating tool use.

Tap any section title below to show or hide the contents of that section.

Please contact the webmaster for detailed information on Web Sketchpad.

How does it feel to move like a dependent variable?

Most students would regard this question as nonsense; they view variables as abstract ideas with no connection to their sensorimotor systems. Though developing students’ understanding of function concepts is a critical goal of secondary mathematics, few students graduate from secondary school possessing a robust conceptualization of function. (Carlson & Oehrtman, 2005) Students have little sense of covariation, their concept image of function is at odds with the formal definition (Vinner & Dreyfus, 1989), and they graph functions without fully understanding the link between the variables and the shape of graph.

Mathematics educators have long stressed the importance of learning by doing, and cognitive scientists research ways in which “cognitive structures emerge from the recurrent sensorimotor patterns that enable action to be perceptually guided.” (Varela et al., 1991, p. 173) Yet our curricula fail to provide students with sensorimotor grounding for function concepts. The primary visual representation that students encounter is the Cartesian graph, which lacks any explicit representation of variables; the other main representation is an equation, such as f(x) = 2x − 3, that lacks any sense of dynamism, any opportunity for students to put variables into motion.

Not surprisingly, students’ difficulties with functions often begin with the concept of variable, which has so many meanings and serves so many purposes that students have difficulty formulating a coherent sense of the term (Schoenfeld & Arcavi, 1998). Freudenthal (1986, p. 494) argues that mathematical variables “are [an] indispensable link with the physical, social, and mental variables,” and observes with approval that “originally ‘variable’ meant something that really varies.” (1986, p. 491) But students seldom experience variables in motion.

If the learning of function begins not with static graphs and equations but rather with variables in motion, with the dance in which independent and dependent variables engage, we argue that students will be able to develop a more detailed and robust concept image of function, and that ideas like relative rate of change, domain, range, composition, and inverse will be better grounded in their sensorimotor experiences. We believe that with such a concept image as a foundation, students can more easily learn to look at a Cartesian graph and visualize the implicit motion of the variables, mentally seeing x move along the horizontal axis while f(x) moves in synchrony along the vertical axis, and that students can even learn to look at an equation like f(x) = 2x – 3 and visualize x in motion, with its dependent variable also in motion, scaled by a factor of 2 and then reduced by 3.

Though geometric transformations are functions that have as their variables points in the plane, transformations have seldom been used to introduce function concepts. (An exception is Coxford and Usiskin’s groundbreaking 1971 text Geometry: A Transformation Approach.) Yet Freudenthal has observed that “Geometry is one of the best opportunities that exists to learn how to mathematize reality….[N]umbers are also a realm open to investigation…but discoveries made by one’s own eyes and hands are more convincing and surprising” (1973, p. 407).

Try it yourself

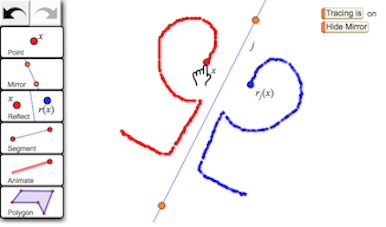
Figure 1: The Reflect Family

Hazzan and Goldenberg note that “The geometric context may provide enough contrast with algebraic contexts to allow essential aspects of the important ideas [of function] to be distinguished from features of the representation.” (1997, p. 287)

In this paper we propose leveraging geometric transformations, supported by dynamic geometry software, to enable students to construct and experience functions in a compelling, memorable way. (We call this approach geometric functions.) Technologically, we use Web Sketchpad software that runs on any modern browser and provides a simplified interface based on tools chosen and customized for each activity.

Figure 2: Student Drawing

Figure 1 previews these innovations. The student begins this Reflect Family activity with a nearly empty screen and six tools on the left. She uses the first three tools to construct and drag independent variable x, to construct a mirror, and to reflect x across the mirror to create the dependent variable r_j(x). (The label r_j(x) has meaning: it stands for “the reflection across j of x.”) She turns on tracing, drags once more, observes the covariation that characterizes this geometric function, and describes its behavior in terms of relative rate of change. [Press the Try it yourself button in Figure 1 to open an interactive websketch in which you can construct and manipulate your own reflect function.]

In the course of this and other related activities, students are encouraged to use the functions they are creating and investigating in order to produce interesting images as in figure 2.

We use a design-based research methodology to iteratively develop, test, and refine the activities described here. (The Design-Based Research Collective, 2003; Barab & Squire, 2004; Fishman et al., 2004) Although earlier versions of some of these activities were developed with the support of the Dynamic Number project funded by the National Science Foundation (Steketee & Scher, 2011), development of the current activities began in earnest in late 2014, when customizable tools became available in Web Sketchpad. We have currently developed 14 activities organized into two units: Introducing Geometric Transformations as Functions (Unit 1) and Connecting Algebra and Geometry Through Functions (Unit 2). To date we have conducted pilot tests with four classes (two at 8th grade and two at 10th grade) located in inner-city Philadelphia schools. (Though designed as an introduction to linear functions, these units appear to be effective even with students who’ve already studied linear functions.) These pilot tests have resulted in substantial changes to the original websketches and student worksheets, and have informed the creation of performance-based assessment instruments both as stand-alone websketches and as pages incorporated into the main activity websketches.

The activities are freely available at geometricfunctions.org/curriculum under a Creative Commons CC-BY-NC-SA 4.0 license, and can be used with any modern web browser. Every activity includes an online websketch and a student worksheet, available both online and as a pdf; we hope to provide detailed teacher-support materials soon. (Due to ongoing revisions, online activities may not exactly match the figures and descriptions in this paper.)

We describe below several of the activities, emphasizing how technology-enabled guided inquiry tasks have enabled students to enact mathematical objects and concepts related to function. We also note several instances in which our pilot testing of the activities has revealed weaknesses in our original instructional design, prompting rethinking and revision of that design.

Try it yourself

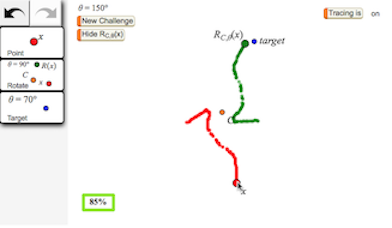
Figure 3: A Rotate Game

The act of dragging geometric function variables can help students develop the sense that variables really do vary. In figure 1 (above) the student constructed and dragged independent variable point x, thus enacting the independent variable.

In figure 3 (part of the Rotate Family activity) she has made a Hit the Target game. After constructing independent variable x and a rotate function to produce dependent variable R_C,θ(x) (the “rotation, about C by angle θ, of x”), she then used the Target tool to make a target and create a challenge: drag x so that dependent variable R_C,θ(x) hits the target. Once the game-player hits the target, she can generate a new problem by pressing the New Challenge button, which changes both the rotation angle θ and the location of the target.

When playing this game, students usually begin either by dragging x toward the target (as in the first part of the red trace) or by adopting a somewhat random guess-and-refine strategy. As they try to improve their play, they are encouraged to reason backward, using the target location and angle θ to approximate the required location for x and guide their initial movement.

Try it yourself

Figure 4: A Dilation Dance

Figure 4 challenges the student to enact the dependent variable of a dilate function: she must drag point y to follow the function rule as independent variable x follows the border of a polygon. Even with hints (the dashed segment and cross-hair showing how close she is, and a traced image of y that changes from red when she’s far away to green when she’s close), this is a real challenge. The player must drag y both in the correct direction and at the correct speed to match the motion of x. In other words, her dragging action must get the rate of change of y relative to x just right.

In these activities, students’ use of points as variables creates and gives meaning to a link between physical movement and mathematical variation. The student drags variables on the plane, observing that it is easy to enact an independent variable; she can drag it wherever she wants. It is much harder to enact a dependent variable, constrained by the rule relating it to its independent variable.

These sensorimotor experiences are enhanced by the close fit between the two-dimensional nature of geometric functions (ℝ²→ℝ² transformations in the plane) and the two-dimensional input and output interfaces (mouse/stylus/finger and screen) that students employ. Similar activities based on one-dimensional dragging using ℝ→ℝ functions tend to be less compelling both visually and due to the mismatch between one-dimensional variables and a two-dimensional computer interface.

Try it yourself

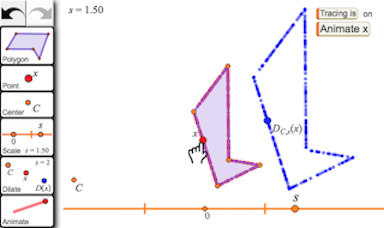
Figure 5: Restrict the Domain

In figures 1 and 3 above, the domain of the function is the entire plane, experienced by the student as the ability to drag x anywhere within the window on the computer screen. This is not in the least remarkable to the student, rendering futile any attempt to introduce the terms domain and range at this stage. To develop conceptual understanding, students should have a meaningful reason to restrict a function’s domain and observe its corresponding range.

In the Dilate Function activity (figure 5) the student uses the Polygon tool to create a polygon and the Point tool to create independent variable x attached to the border of the polygon. She drags x to explore what happens, and how it feels, when x is restricted to this polygonal domain. After using the Dilate tool to dilate x about center point C by scale factor s, the student turns tracing on and drags x again to observe the corresponding range traced out by the dependent variable D_C,s(x).

Figure 6: Sample Student Work (Dilate Family)

The act of dragging x on its restricted domain while attending to both the path and the relative rate of change of D_C,s(x) are important sensorimotor experiences that provide students with grounding for their conceptual understanding of domain, range, and relative rate of change while also spurring them to consider what it means to apply a function all at once to an entire set of points (a polygon).

By the end of Unit 1 (Introducing Geometric Transformations as Functions), students in the pilot test were effectively using the tools and identifying the roles of the various objects. Most were already quite comfortable describing function behavior in terms of relative rate of change (both speed and direction), as illustrated in figure 6.

Try it yourself

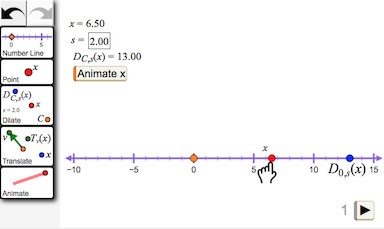
Figure 7: Transform on the Number Line

Unit 2 (Connecting Algebra and Geometry Through Functions) explicitly connects the geometric functions of Unit 1 to algebra. It begins by asking students to restrict the domain of these geometric transformations to a number line and to determine which of the “Flatland” (two-dimensional) function families can most easily fit into the “Lineland” (one-dimensional) environment of the number line. (Abbott, 1886) Once students have determined that the dilate and translate families are particularly suitable because their independent and dependent variables always move in the same direction, students engage in construction activities that connect the geometric behavior of dilation and translation to the observed numeric values of their variables on the number line.

In figure 7 the student uses Number Line, Point, and Dilate tools to create a point restricted to the number line and dilate it about the origin. She measures the coordinates of x and D_0,s(x) and drags x to compare the values and describe the relative rate of change numerically. (“When I increase x by 1, D_0,s(x) increases by 2 times as much, which is the same as the scale factor s.”) By experimenting with different scale factors, she concludes the coordinates produced by this dilation satisfy D_0,s(x) = x·s. She then experiments with translation restricted to the number line and concludes that translation by a vector of directed length v satisfies the equation T_v(x) = x + v. Thus she concludes that dilation on the number line corresponds to multiplication, and translation corresponds to addition.

Try it yourself

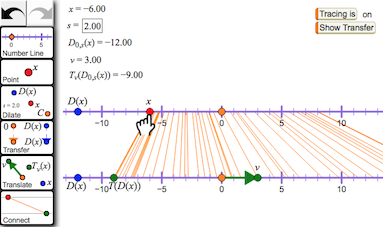
Figure 8: Create a Dynagraph

Our student, having moved from Flatland to Lineland and discovered special meanings of dilation and translation on the number line, is now ready for a new task: What happens when you dilate x and then translate the dilated image; in other words, how does T_v(D_0,s(x)) behave? (Ideally this is the student’s first experience with linear functions, and she herself will invent the term “linear function” after completing the tasks described below.) Her first effort to enact this task becomes visually confusing, with three variables and a vector stumbling over each other on the same number line. To alleviate the confusion, the next activity incorporates a Transfer tool that moves the dependent variable to a different number line, separate from but aligned with the first.

In figure 8 the student has used such a tool to construct a second number line parallel to the original, creating a dynagraph (Goldenberg, Lewis, & O’Keefe, 1992). By varying x and observing the connecting line between the variables, the student describes and explains how changing each parameter (scale factor s and vector v) affects the relative rate of change of the variables and their relative locations.

Try it yourself

Figure 9: Create a Cartesian Graph

In the final activity of Unit 2 students create the Cartesian graph of a linear function using geometric transformations. (Numbers are used only to determine the scale factor for dilation and to measure the locations of variables on their number lines.)

As figure 9 illustrates, students start with the same initial tools that they used to create a dynagraph, but this activity’s Transfer tool rotates a variable to a vertical number line perpendicular to the original (horizontal) number line. After using this tool to rotate D_0,s(x) to the vertical line and translating by vector v, the student uses the x-value and y-value tools to construct lines that keep track of the horizontal location of x and the vertical location of T_v(D_0,s(x)). She then constructs a traced point at the intersection of these horizontal and vertical lines and drags x to see how the traced point’s motion corresponds to the behavior of the two variables.

Figure 10: Inferring Motion from a Graph

After performing the construction, the student tries different values for the scale factor s and the translation vector v, and observes how changing the scale factor affects not only the speed of T_v(D_0,s(x)) relative to x, but also the shape of the traced line.

For instance, one of our pilot test students looked at the lower traces shown in figure 10 and explained that the this trace clearly indicated that the variables were moving in opposite directions, because the value of the dependent variable was moving down as the independent variable moved right. She went on to say that T_v(D_0,s(x)) was clearly decreasing more slowly than x was increasing, because the traces didn’t go down as quickly as they went to the right. Observations like this suggest that students can indeed use their experiences in geometrically enacting variables and functions to visualize the motion implicit in a static Cartesian graph.

Try it yourself

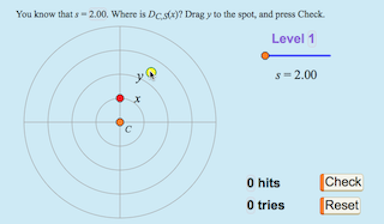
Figure 11: Dilate Games

Our pilot tests have also helped us generate ideas for performance-based assessments. For instance, we created the dilate-family game shown in figure 11 as we discussed assessment issues with one of our pilot-test teachers. The game has multiple levels that require greater precision and provide less diagrammatic scaffolding as a student moves up through the levels. We intentionally did not set a specific number of problems per round, so that a teacher has the flexibility to say (for instance) “To be a dilation apprentice, you must score 8 of 10 at Level 2; to be a dilation master, you must score 7 of 10 at Level 5; and to be a dilation super-hero you must score 16 of 20 at Level 9.”

We are not yet satisfied with students’ results on this dilation-family assessment; some students who had constructed and investigated dilate functions successfully still had difficulty understanding how the game worked, even at Level 1. We have already refined the activity itself to better support students’ transition to the game, but remain concerned about possible gaps in students’ visualization of the dilation function. In a coming pilot test we will explore this further by interviewing small groups of students, and make additional revisions based on what we learn. (We also plan to modify the game to enable direct reporting of students’ results to the teacher. The initial version relies either on visual inspection by the teacher or on screen captures submitted by students.)

Try it yourself

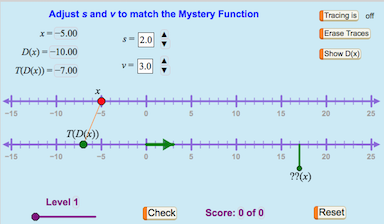
Figure 12: Dynagraph Game

Figure 12 illustrates the Dynagraph Game, a performance-based assessment for the dynagraph activity described above. In this game independent variable x is always in motion from left to right, and students adjust s and v to control the dynagraph whose dependent variable is T(D(x)). There is also a “mystery function” whose moving dependent variable ??(x) is shown below the lower axis. The student’s challenge is to adjust s and v to match the mystery function, so that T(D(x)) is exactly aligned with ??(x). Higher levels of the game require greater precision in adjusting s and v.

We conjecture that performance-based assessments such as these can help students solidify their understanding of function concepts while also promoting mathematical fluency, and we are eager to test this conjecture as we continue our effort to refine the activities based on classroom testing.

By using web-based dynamic math software and tools tailored to carefully-structured tasks, students can enact geometric transformations as functions, creating them, manipulating them, and experimenting with them. Students can vary the variables, describe their relative rate of change, create and use restricted domains, compose transformations, discover connections between geometry and algebra, and construct and shed light on the Cartesian graph of a linear function, while simultaneously developing a solid understanding of geometric transformations.

Our early testing suggests that this approach will enable students to connect geometry and algebra as they ground function and transformation concepts in their sensorimotor experience, and we look forward to further refining the activities and to verifying their effectiveness with a wide variety of students.