Geometric Functions
▿ Overview
Use this page to explore multiplying two binomials. Part 1 includes binomials with positive constant terms, like these:
- `(x + 3)(x + 5)` on page 1
- `(2x + 5)(3x + 2)` on page 2
Part 2 includes binomials with constant terms that can be either positive or negative, with problems like these:
- `(x + 3)(x - 5)` or `(x - 1)(x + 4)` on page 1
- `(2x - 5)(3x + 2)` or `(3x - 2)(2x - 8)` on page 2
▹︎ Binomial Multiplication Part 1
Download the student worksheet.
Download the teacher notes.
![]() Play the how-to video
Play the how-to video
In this activity you can drag the sliders to change the binomials.
Page 1: Drag the top orange slider to make the top of the rectangle correspond to one binomial, and drag the left orange slider to make the left side correspond to the other binomial.
Page 2: Drag the top green and orange sliders to match one binomial, and drag the left grren and orange slider to match the other.
Use the dark red sliders on the left to adjust the sizes of the tiles.
▹︎ Binomial Multiplication Part 2
Download the student worksheet.
Download the teacher notes.
![]() Play the how-to video
Play the how-to video
In this activity you can manipulate the sliders to rearrange algebra tiles.
Drag the sliders to make the width correspond to one binomial and to make the height correspond to the other binomial.
You can drag the orange sliders for the constant terms in either direction, depending on whether the constant term is positive or negative.
Use the dark red sliders on the left to adjust the sizes of the x tile and the unit tile.
▹︎ Follow Up
Once students have mastered the use of these virtual algebra tiles, follow-up activities like those suggested here can help them generalize this method. Be careful as you move from one of these models to the next; moving too quickly can impede students’s ability to generalize and to connect one model with the next.
Draw Your Own Tiles: Solve similar problems by drawing your own algebra tiles on paper, like this:
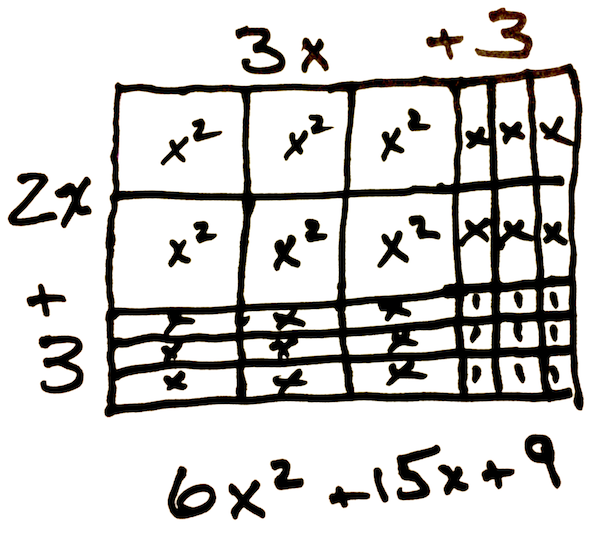
When you need to draw negative tiles, you can use a highlighter to identify all the negative tiles.
Just Draw the Boxes: As you get comfortable with the draw-your-own-tiles method, you can save time by making a drawing like this:
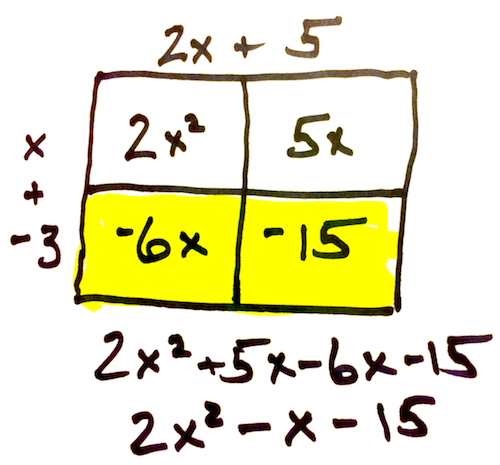
In this model the four boxes represent the four regions of algebra tiles in the sketches above. Notice that the boxes that contain negative tiles have been marked using a highlighter.
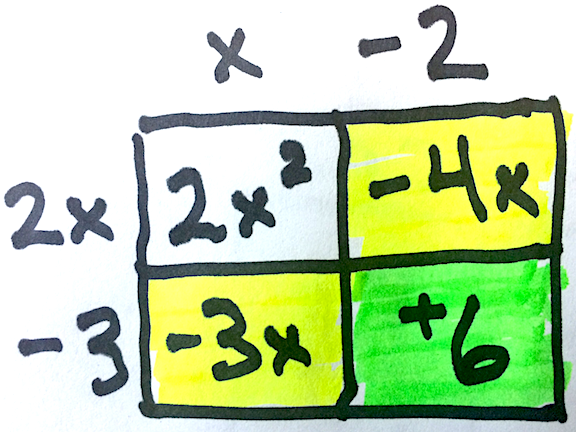
Using two highlighting colors makes it easy to distinguish boxes that have been “doubly subtracted” and need to be added back into the sum.
Multiply Higher-Order Polynomials: One of the biggest advantages of this approach over the FOIL method is that it’s easily extended to multiplying any two polynomials.
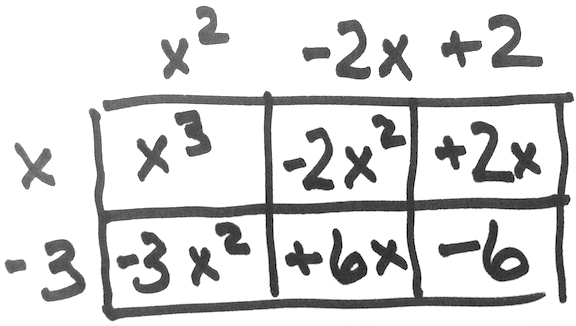
▹︎︎ The Fine Print
Requirements:
These activities require web access using a browser that supports HTML5 and JavaScript. (That means almost any current browser.) No purchase is required, and there’s no advertising anywhere.
Release Information
[an error occurred while processing this directive]Update History:
