
Introduction
Unit 1: Introducing Functions Geometrically
Identify Functions
In this lesson students distinguish independent from dependent variables, describe the behavior of dependent variables as they drag the independent variable, distinguish between functions and non-functions, and arrive at their own definition of function. The examples include some problematic cases, stimulating students' discussion and argumentation.
Identify Function Families
In this lesson students drag variables to solve “Which one is different” puzzles involving four functions, three of which are from the same family. They begin by comparing the shapes of traces left by the variables, analyze the relationship between the traced shapes and the rate of change of the variables, and learn to distinguish functions based on rate of change. Students have their first encounter with function notation, as a way of indicating which dependent variable is related to which independent variable.
The Reflect Family
In this lesson students begin with a challenge of threading a maze. They create reflection designs, they play reflection games, they use restricted domains, and they describe reflections using function notation. Students create and perform original reflection dances.
Note th instructional design of the lesson web pages: everything is in one place, with the vanilla page showing the student the entire lesson outline in an easily-navigated format, and with support materials available for the teacher (T), an enhanced version with more background and pedagogical detail for the preservice or PD workshop teacher (P), and an additional level of support for the university professor or workshop facilitator (F).
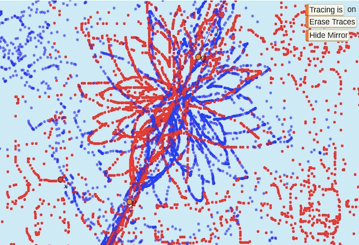
Reflect Family Results

The Rotate Family
In this lesson students create rotate functions, formulate informal descriptions of the rate of change that distinguishes rotate functions, use function notation, and restrict the domain of a rotate function to observe the corresponding range. Students perform physical and virtual function dances, they solve puzzles requiring them to rotate one shape to superpose it upon another congruent shape, and they use multiple rotations to create interesting designs. Students play a video game in which they're given three of the four elements of a rotate function (independent variable, center of rotation, angle of rotation, dependent variable), and their job is to find the value or location of the missing element.
Geometric-Function Dance Project
In this lesson students choreographed and video-recorded their own function dances incorporating the various transformations they studied in Unit 1.
Unit 3: Congruence Proofs by Construction
4a Prerequisites
4b Segment Congruence
If two segments are of equal length, how can we prove that one segment can be superposed on the other?
4c SSS Triangle Congruence
If two triangles have corresponding sides that are equal in length, how can we prove that one triangle can be superposed on the other?
Unit 4: Connect to Cartesian
In these activities students restrict the domain of the geometric functions to a line, number the line, and discover some exciting connections between geometry and algebra. As they explore these connections they play some enjoyable and challenging games, explore exciting mathematics, construct a dynagraph, and conclude by using geometric transformations to create the Cartesian graph of a general linear equation.
Recent WSP Enhancements
In addition to the here are a c
The Fine Print
Requirements:
These activities require web access using a browser that supports HTML5 and JavaScript. (That means almost any current browser.) No purchase is required, and there’s no advertising anywhere.
Release Information
[an error occurred while processing this directive]Update History:
Record every major revision, in reverse chronological order
24 Jan 2018: Created this lesson template.

